Electric field due to an infinite plane sheet of charge.
Let us consider an infinite thin plane sheet of positive charge having a uniform surface charge density \(\sigma\). Let P be the point where electric field E is to be found. Let us imagine a cylindrical gaussian surface of length 2r and containing P as shown. The net flux through the cylindrical gaussian surface.
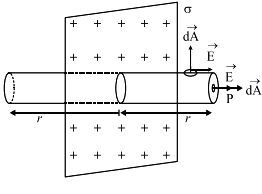
\(\phi = ∮\vec e.\overrightarrow{dA}\)
\( =\underset{RCF}\int \vec E.\overrightarrow{dA}+ \underset{LCF}\int\vec E.\overrightarrow{dA} + \underset{CS}\int \vec E.\overrightarrow{dA}\)
\( = \underset{RCF}\int EdA \cos0^\circ + \underset{LCF}\int EdA\cos^\circ + \underset{CS}\int EdA\cos90^\circ\)
= E A + EA + 0
\(\phi\) = 2 EA ...(1)
Here A is the area of cross-section of each circular facei.e. LCF and RCF. The total charge enclosed by the gaussian cylinder
\( = \sigma A\ ...(2)\)
Using Gauss’s theorem, from (1) and (2),
\(2\ EA = \frac{\sigma A}{\varepsilon_0}\)
\(E = \frac{\sigma}{2\varepsilon_0}\)