Question

Tangents And Normals of Derivatives

Answer 1

In this section we shall use differentiation to find the equation of the tangent line and the normal line to a curve at a given point.

A line which touches the curve at a single point is called tangent at a point and if a line is perpendicular to the tangent at the point of contact, then it is called normal.

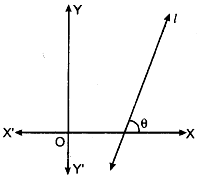
Slope of a line: The trigonometrical tangent of the angle that a line makes with the positive direction of X-axis in anti-clockwise direction is called the slope or gradient of the line. The slope of line is generally denoted by m.

Thus, slope of line m = tan θ

Slope of line by equation of line:

Let equation of line be ax + by + c = 0, then slope of line is m such that:

m = \(\frac{-a}{b} = - \frac{\text {coefficient of x}}{\text{coefficient of y}}\)

Note that the slope of the tangent to the curve y = f(x) the point (x₀, y₀) is given by \(\frac{dy}{dx}]_{x_0,y_0}\) = f'(x₀)). So the equation of the tangent at (x₀, y₀) to the curve y = f (x) is given by

Also, since the normal is perpendicular to the tangent, the slope of the normal to the curve y = f (x) at (x₀, y₀) is \(\frac{-1}{f'(x_0)}\) if f' (x₀) ≠ 0.

Therefore, the equation of the normal to the curve y = f(x) at (x₀, y₀) is given by 

y - y₀ = \(\)\(\frac{-1}{f'(x_0)}\) (x -x₀)

i.e (y - y₀)f' (x₀) + (x - x₀) = 0

Note:

If a tangent line to the curve y = f(x) makes an angle θ with x-axis in the positive direction, then \(\frac{dy}{dx}\) = slope of the tangent = tan θ.

Particular cases

• If slope of the tangent line is zero, then tan θ = 0 and so θ = 0° which means the tangent line is parallel to the x-axis. In this case, the equation of the tangent at the point (x₀, y₀) is given by y = y₀.
• If, θ = \(\frac{\pi}{2}\) then tan θ = ∞, which means the tangent

line is perpendicular to the x-axis, i.e., parallel to the y-axis. In this case, the equation of the tangent at (x₀, y₀) is given by x = x₀.