दिया है : \(\triangle \mathrm{PQR}\) जिसमें \(\mathrm{BC}=7 \mathrm{~cm}, \angle \mathrm{Q}=45^{\circ}\) व \(\angle \mathrm{P}=105^{\circ}\)
रचना करनी है : एक अन्य तिभिन की जिसकी भुजाएँ \(\triangle \mathrm{PQR}\) की संगत भुजाओं की \(\frac{4}{3}\) गनी हो।
रचना विधि:
1. रेखाखण्ड \(\mathrm{QR}=8 \mathrm{~cm}\) खींचे।
2. QR के बिन्दु Q पर QR से \(45^{\circ}\) का कोण बनाती हुई एक रेखा QZ खींची।
3. QR के दूसरी ओर Q पर 9 R से \(105^{\circ}\) के कोण पर रेखा QD खींची।
4. QD के बिन्दु Q पर QD से समकोण बनाती हुई एक रेखा QX खींची।
5. QR का लम्ब समद्विभाज खींचा जो QX को बिन्दु O पर काटती है।
6. O को केन्द्र मानकर OQ त्रिज्या से वृत्तखण्ड QPR खींचा जो QZ का बिन्दु P पर काटता है।
7. PR को मिलाकर \(\triangle \mathrm{PQR}\) प्राप्त किया।
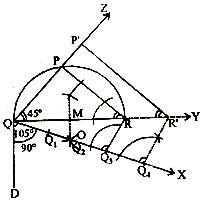
8. QX में 4 समान खण्ड \(\mathrm{QQ}_{1}, \mathrm{Q}_{1} \mathrm{Q}_{2}, \mathrm{Q}_{2} \mathrm{O}_{3}\) व \(\mathrm{Q}_{3} \mathrm{Q}_{4}\) खींचे।
9. रेखाखण्ड \(Q_{3} R\)।
10. बिन्दु \(Q_{4}\) से \(Q_{4} R^{\prime}\) समान्तर \(Q_{3} R\) खींची जो बढ़ी हुई \(Q R\) को \(R^{\prime}\) पर काटती है।
11. \(\mathrm{R}^{\prime}\) से \(\mathrm{R}^{\prime} \mathrm{P}^{\prime}\) समान्तर PR खींची जो QZ का \(\mathrm{P}^{\prime}\) पर काटती है।
\(\triangle \mathrm{P}^{\prime} \mathrm{QR}^{\prime}\)अभीष्ट त्रिभुज है।
औचित्य : क्योंकि \(\mathrm{QQ}_{4}, \mathrm{QQ}_{3}\) की \(\frac{4}{3}\) गुनी है और \(\mathrm{QR} \| \mathrm{Q}, \mathrm{R}^{\prime}
\)
\(\therefore \mathrm{QR}, \mathrm{QR}\) की \(\frac{4}{3}\) गुनी होगी।
\(\because \mathrm{P}^{\prime} \mathrm{R}^{\prime} \| \mathrm{PR}\) और \(\mathrm{QR}^{\prime}=\frac{4}{3} \mathrm{QR}^{\prime}\)
\(\therefore \mathrm{P} Q\) भी PQ की \(\frac{4}{3}\) गुनी है।
\(\therefore \quad \frac{P^{\prime} \mathrm{Q}}{\mathrm{PQ}}=\frac{\mathrm{P}^{\prime} \mathrm{R}^{\prime}}{\mathrm{PR}}=\frac{\mathrm{QR}^{\prime}}{\mathrm{QR}}=\frac{4}{3}\)