The Biot-Savart law asserts magnetic field dB due to an element dI carrying a steady current i at a point p at a distance r from the current element is
\(dB = \frac{\mu_0}{4\pi}i = \frac{dl\times r}{r^3}\)
Study fig. carefully. To obtain the total field at \(P_1\) we must integrate this vector expression over the entire length of the conductor.
Expression for the magnetic field at the centre of a current carrying circular loop: Suppose that RS is a circular loop and I is fitting by this. On it centre so find out value of magnetic field it device in little parts cause at dl little part magnetic field on centre
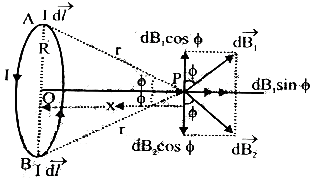
\(dB = \frac{\mu_0}{4\pi}\times \frac{Idl\sin \theta}{r^2}\)
Here \(\theta = 90^\circ, \sin \theta = 90^\circ =1; \ dB = \frac{\mu_0}{4\pi}.\frac{Idl}{r^2}\)
Cause of all loop magnetic field
\(\int dB = \frac{\mu_0}{4\pi}.\frac{I}{r^2}\int dl\ or \ B = \frac{\mu_0}{4\pi} \frac{1}{r^2}.2\pi r \ or\ B = \frac{\mu_0I}{2r} \)
If number of in twists in the loop then \(B = \frac{\mu_0nI}{2r}\).