For normal modes of oscillations, both the degrees of freedom, namely x1 and x2 oscillate with the same frequency and they oscillate in phase or out of phase with one another:
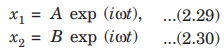
where A and B are in general complex to take account of the possibility that x1 and x2 might oscillate out of phase with one another. Substituting Eqns. (2.29) and (2.30) into Eqns. (2.27) and (2.28), we get

This is a quadratic equation in the variable ω2. It has two solutions in general, which

where A1 and A2 are arbitrary constants and ω1 and ω2 are the normal mode frequencies. Normal coordinates: If the differential equations are coupled, we have to search for new variables which satisfy uncoupled differential equations. The new variables are then called normal coordinates. Suppose X and Y are the normal coordinates satisfying the differential equations

If X and Y are the normal coordinates, then any constant multiple of X and Y also satisfy Eqns. (2.35) and (2.36). Suppose X and Y are obtained from the linear combinations of x1 and x2 so that we may write
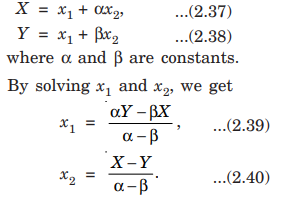
We substitute Eqns. (2.39) and (2.40) into Eqns. (2.27) and (2.28) and separate the uncoupled differential equations for X and Y, which give

Thus α and β satisfy the same quadratic equation having the roots
