Question

A mass m slides on a  rotating frictionless and massless rod S such that it is pressed against a rough circular wall (coefficient of friction µ). If the mass starts in contact with the wall at a velocity v0, how many rotations will it take for its velocity to drop to v₀/10?

Answer 1

If we express the acceleration vector in terms of the Serret-Frenet frame, then the equations of motion are written as

Note that the weight of the mass does not influence the motion since the motion takes place in a horizontal plane. If we use the kinematic relations a_t = ˙v, a_n = v²/r, and the friction law R = µN we can write the first equation of motion in the form

mv˙ = −µm v²/r

Separation of variables and integration yield

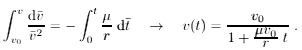
We integrate again to obtain the distance traveled:

Now we calculate the time t₁ that it takes for the velocity to drop to v₀/10:

The corresponding value s(t₁) is found as

This yields the corresponding number of rotations: