Question

Using Bohrs quantization rule, derive a formula for electrons speed in the quantized Bohrs orbits. By putting in the values of constants, explicitly derive the value of electrons speed in n = 1 orbit. What fraction of speed of light it is? Is it justified to treat electrons motion as non-relativistic in Hydrogen atom as we have been doing? What happens to the speed in higher levels?

Answer 1

The basic feature of quantum mechanics that is incorporated in the Bohr Model the energy of the particles in the Bohr atom is restricted to certain discrete values. One says that the energy is quantized. This means that only certain orbits with certain radii are allowed; orbits in between simply don’t exist.

In the Bohr model, the wavelength associated with the electron is given by the DeBroglie relationship,

λ = h/mυ,

and the standing wave condition that circumference = whole number of wavelengths. In the hydrogenic case, the number n is the principal quantum number.

2πr = nλ.

These can be combined to get an expression for the angular momentum of the electron in orbit. (Note that this assumes a circular orbit, a generally unwarranted assumption.)

The electron is held in a circular orbit by electrostatic attraction. The centripetal force is equal to the Coulomb force.

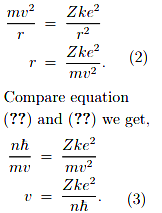
where 

Z = Atomic number for Hydrogen = 1 

k = Coulomb’s constant = 9 × 10⁹ Nm²/C² 

e = Charge on an electron = 1.6 × 10⁻¹⁹ C 

h = Reduced Planck’s constant = 1.05 × 10⁻³⁴ J.s

By putting in the values of constants, electron’s speed will be,

This speed of electron can be compared to the speed of light by taking ratio to these two speeds.

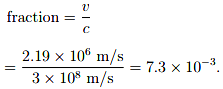
This is justified to treat this electron’s motion as non-relativistic because the speed of electron is not comparable to the speed of light rather it is pretty small. 

From equation (??) we can see that v ∝ 1/n, therefore v decreases as n increases.