Question

Prove that the polar locus of the current drawn by a circuit of constant reactance and variable resistance is circular when the supply voltage and frequency are constant. If the reactance of such a circuit is 25 Ω and the voltage 250, draw the said locus and locate there on the point of maximum power and for this condition, find the power, current, power factor and resistance. Locate also the point at which the power factor is 0.225 and for this condition, find the current, power and resistance.

Answer 1

For the first part, please refer to

Radius of the current semi-circle is = V/2X = 250/2 × 25 = 5 A. 

As discussed in , point A [Fig.] corresponds to maximum power. 

Now, I_m = V/X  = 250/25 = 10A; P_m = 1/2 x 250 x 10 = 1250 W 

Current OA = I_m/√2 = 10/√2 = 7.07 A ; p.f. = cos 45° = 0.707. 

Under condition of maximum power, R = X = 25 Ω

Now, cos θ = 0.225 ; 

θ = cos^–1 (0.225) = 77°

In Fig., current vector 

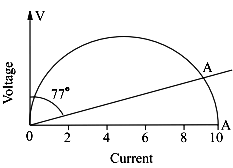
OA has been drawn at an angle of 77° with the vertical voltage vector OV. By measurement, current OA = 9.74 A 

By calculate, OA, = I_m cos 13° = 10 × 0.974 = 9.74 A 

Power = VI cos θ = 250 × 9.74 × 0.225 = 548 W 

P = I²R; R = P/I² = 548/9.74² = 5.775 Ω