Question

Find the positive integers x and y such that x + y = 60 and xy³ is maximum.

Answer 1

Given x + y = 60 

⇒ y = 60 – x 

Let S = xy³ 

= x (60 – x)³

ds/dx = x . 3(60 – x)² (0 – 1) + (60 – x)³ . 1

= –3x(60 – x)² + (60 – x)³ 

= (60 – x)² + (–3x + 60 – x) 

= (60 – x)² (60 – 4x)

ds/dx = 0 ⇒ (60 – x)² (60 – 4x) = 0

⇒ 60 – 4x = 0 

⇒ 4x = 60 

⇒ x = 15

d²s/dx² = (60 – x)² (–4) + (60 – 4x) 2 (60 – x) (–1)

= – 4 (60 –x)² – 2 (60 – 4x) (60 – x)

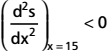
∴ S is maximum at x = 15 

∴ y = 60 – 15 = 45 

Hence x = 15, y = 45.