Question

(a) Derive an expression for the electric field at any point on the equatorial line of an electric dipole.

(b) Two identical point charges, q each, are kept 2 m apart in air. A third point-charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.

Answer 1

(a) Electric field intensity at point P due to + ve q charge at point P

Electric field intensity at point P due to - ve q charge at point P

E_+qsinθ and E_−qsinθ are equal in magnitude and oppsite in direction so they cancel out.

Net electric field at point P

(b) As charge θ is in equilibrium net force on the charge θ is zero

Hence, Q is at the mid point of the line joining the charge q and q. 

As the whole system is also in equilibrium, force an the charge q must also be zero.

Answer 2

(a) Electric field at point on equatorial line of an electric dipole.

Consider on electric dipole consisting of two point-charges +q and –q separated by distance 2a.

Let P be a point at a distance r from the center of the dipole on the equatorial line, where the electric field is to be calculated.

Let E₁ be electric field intensity at P due to charge –q. Therefore,

From right-angled triangle AOP, we have AP = √r² + a² . Therefore, 

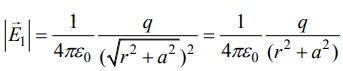
The direction of Vector E₁ is along PA.

Now, let E₂ be electric field intensity at P due to charge +q.

From right-angled triangle BOP, we have BP = √ r² + a².There fore,

The direction of E₂ is along BP.

The resultant electric field Vector E is the difference of the two fields:

Thus, the electric potential due to electric dipole is zero at every point on the equatorial line of the dipole.

(b) The two identical charges are kept 2 m apart. 

A third charge Q is placed on line joining the charges such that the system is in equilibrium. Let this charge be placed at distance x from charge A. Since the system is in equilibrium, the Coulomb force experienced by charge at point B from charge at A and C must be equal and opposite. Force on charge q at B due to charge q at A is

Force on charge q at B due to charge Q at C will be

Therefore,

Also, the force experienced by charge Q at point C due to charge q at point A and charge q at point B must be equal. The force on charge Q due to charge q at point A is

Force on charge Q due to charge q at point B is

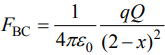
Therefore,

Using x = 1 m in Eq. (1), we get

Thus, the charge  Q = -q/4 is placed at 1 m, that is, the charge Q is placed at the middle of the two charges q.