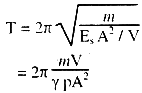Question

An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released, it executes S.H.M. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal.

Answer 1

(i) When the ball of mass 'm' is depressed by a small distance y, let the volume of air decreases by W Δv while pressure increase by Δp.

For isothermal change, according to Boyle's law,

pV = (p + Δp)(V - Δv)

or, pV = pV + ΔpV - pΔv - ΔpΔv

For Negative pv, we have

pΔv = ΔpV

or, p = {ΔpV}/{Δv} = {Δp}/{Δv/V} 

= Stress/Volume strain

= E_T [isothermal bulk modulus]

We have Stress = Δp = E_T Δv/V

or, Force/Area = E_T Δv/V

or, F/A = F_TΔv/V ⇒ F = F_TΔvA/V

or, F = F_TΔvA/V

But, change in volume

v = Ay

Hence, F = E_TA²/V y

Comparing it with F = Ky, we get

F = E_TA²/V

Hence, the time period,

(ii) For adiabatic change, according to Poisson's law,

pV = (p + Δp) (V - Δv)'

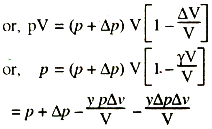
Neglecting γΔpv/V, we get

γΔpΔv/V = Δp

γp = {y}/{v/V} = {Stress}/{Volume strain} = E_s (Adiabatic Bulk modulus)

∴ E_s = γΔp

Again the time period is similarly given by