See Fig.
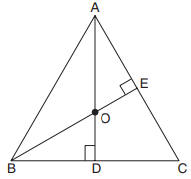
Let A, B and C be the vertices
A ≡ [at1t2, a(t1 + t2)]
B ≡ [at2t3, a(t2 + t3)]
C ≡ [at3t1, a(t3 + t1)]
The slope of BC is

The slope of altitude AD = −t3. The equation of AD is
a(t1 + t2) = –t3(x – at1t2) ......(1)
Similarly, the equation of altitude BE is
y – a(t2 + t3) = –t1(x – at2t3) ....(2)
The coordinates of orthocentre O are obtained by simultaneously solving Eqs. (1) and (2). Subtracting Eq. (2) from Eq. (1), we get
a(t3 – t1) = −x(t3 – t1) ⇒ x = –a
Subtracting x = −a in Eq. (1), we get
y = a(t1 + t2) – t3(–a – at1t2)
y = a(t1 + t2 + t3 + t1t2t3)
The coordinates of the orthocentre does not depend on the values of t1, t2 and t3.