Question

Show that each one of the following systems of linear equations is consistent and also find their solutions:

(i) 6x + 4y = 2

9x + 6y = 3

(ii) 2x + 3y = 5

6x + 9y = 15

Answer 1

(i) Given as 6x + 4y = 2

9x + 6y = 3

The given equation can be written in matrix form

Here

|A| = 36 – 36 = 0

Therefore, A is singular, Now X will be consistence if (Adj A) x B = 0

C₁₁ = (– 1)^{1 + 1} 6 = 6

C₁₂ = (– 1)^{1 + 2} 9 = – 9

C₂₁ = (– 1)^{2 + 1} 4 = – 4

C₂₂ = (– 1)^{2 + 2} 6 = 6

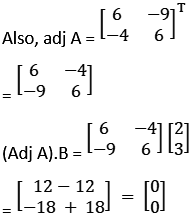
So, AX = B will be infinite solution.

Suppose y = k

So,

6x = 2 - 4k or 9x = 3 - 6k

X = (1 - 2k)/3

So, X = (1 - 2k)/3 and Y = k.

(ii) Given as 2x + 3y = 5

6x + 9y = 15

Here

|A| = 18 – 18 = 0

Therefore, A is singular,

Then X will be consistence if (Adj A) x B = 0

C₁₁ = (– 1)^{1 + 1} 9 = 9

C₁₂ = (– 1)^{1 + 2} 6 = – 6

C₂₁ = (– 1)^{2 + 1} 3 = – 3

C₂₂ = (– 1)^{2 + 2} 2 = 2

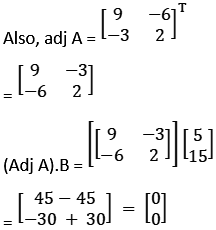
So, AX = B will be infinite solution.

Suppose y = k 

So,

Therefore, X = (5 - 3k)/2, Y = k