Question

Derive σ = \(\frac{ne^2\tau}{m}\) Where the symbols have their usual meaning.

Answer 1

Consider conductor of length _∆x, area of cross section A. 

V_d = drift speed of free electrons, in a time _∆t, let all the electrons travel a distance _∆x = V_{d ∆}t. 

Electric current I = _∆Q /_∆t = neAv_d 

The acceleration acquired by the free electrons is given by a = \(\frac{-eE}{m}\)

where m = mass of the electron 

If τ = relaxation time then velocity 

v_d = \(\frac{-eE}{m}\tau\)

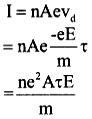
Current density J = \(\frac{1}{A}\), J = σE therefore

σ = \(\frac{ne^2\tau}{m}\)