Question

A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimensions of the rectangular part of the window to admit maximum light through the whole opening.

Answer 1

Suppose the radius of semicircle, length and breadth of rectangle be r, x and y respectively

AE = r

AB = x = 2r(semicircle is mounted over rectangle) …1

AD = y

Given as the perimeter of window = 10 m

x + 2y + πr = 10

2r + 2y + πr = 10

2y = 10 – (π + 2).r

y = (10 - (π + 2)r)/2 ...(2)

To admit the maximum amount of light, area of the window should be maximum 

Assuming the area of window as A

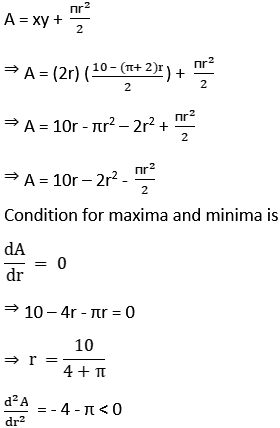
For the r = 10/(4 + π) A will be the maximum.