Question

What is a spherical capacitor? Obtain the relation for capacitance of a spherical capacitor.

Answer 1

Capacitance of an Isolated Spherical Conductor:

Suppose an isolated spherical conductor of radius R is placed in a medium of dielectric constant K. If on giving a charge q, its potential becomes V, then
V = \(\frac{1}{4 \pi \varepsilon_{0} K} \frac{q}{R}\)

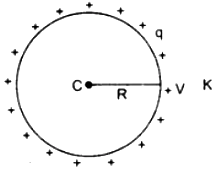
Therefore capacitance of spherical conductor,

i.e., “the capacitance of spherical conductor is directly proportional to its radius.”
If C_m is the capacitance of the spherical conductor when it is placed in a medium of dielectric constant K and C₀ when placed in vacuum or air, then,

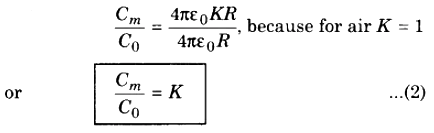
i.e., dielectric constant of a medium is defined as the ratio of capacitance of a conductor placed in that medium and capacitance of same conductor when placed in air.