Refraction through Spherical Surface:
Refraction through spherical surfaces also obey the same laws as for plane surfaces.
Sign convention of co-ordinate geometry for measuring the distances from spherical surfaces:
1. The rays of light are always incident on spherical surface from left side.
2. For spherical surface all the distances are measured from pole along the principal axis.
3. The distances measured in the direction of incident ray are taken as positive.
4. The distances measured in opposite direction of incident ray are taken as negative.
5. The lengths of object and image are taken as positive on the upper side of principal axis and negative on the lower side of principal axis.
Formula for refraction of convex spherical surface:
Suppose AB is a convex spherical surface, on the left side of which there is one medium (rarer) and on the right side the second medium (denser). P is the pole of the spherical surface and C is its centre of curvature. According to ray diagram of fig, I is the image of the object O. The normal drawn from point M on principal axis is MP’.
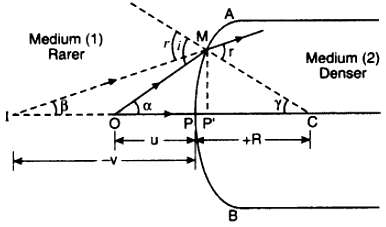
According to Snell’s law,
1n2 = \(\frac{\sin i}{\sin r}\)
Where 1n2 = the refractive index of medium (2) with respect to medium (1).
n = \(\frac{\sin i}{\sin r}\)
(on taking n in place of 1n2 temporarily) If the angles i and r are very small, then
sin i ≈ i and sinr ≈ r
∴ n = \(\frac{i}{r}\)
or i = nr …………. (1)
∴ In triangle, the exterior angle is equal to sum of the opposite two interior angles.
∴ From ∆MOC, i = α + γ ………. (2)
And from ∆MIC,
r = β + γ ………… (3)
Substituting the value of i and r in equation (1), then we get,
(α + γ) = n (β + γ) ……….. (4)
If point M is not far from the principal axis, then
(i) Points P and P’ are very close to each other and considered to be same point.
(ii) Angles α, β and γ will be small.
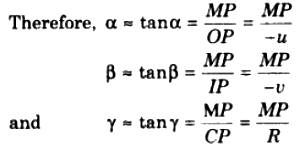
Now, substituting the values of α, β and γ in equation (4) then, we get

This formula is known as ‘Refraction Formula’ of convex surface. If the absolute refractive indices of medium 1 and 2 be n1 and n2 respectively, then
