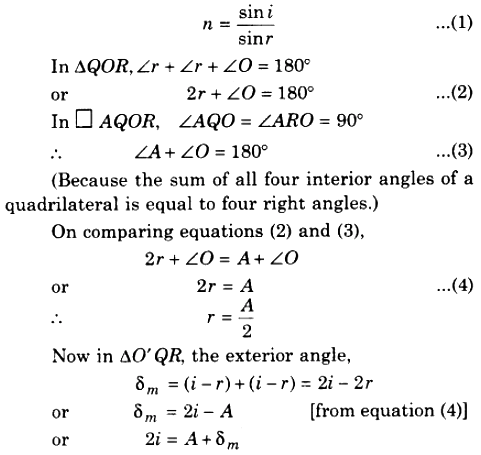Refraction in Prism:
When a light-ray refracts through the prism, following two actions are possible ;
1. Deviation
2. Dispersion
1. Deviation by Prism: When a monochromatic ray of light incidents on the refracting surface of the prism, then the ray refracts two times and hence the direction of the ray gets deviated (fig). “The angle between the directions of incident ray and emergent ray is known as the angle of deviation.”
In diagram it is shown by δ.
In fig.
PQ = incident ray; QR = refracted ray; RS = emergent ray; i1 = angle of incidence; r1 and r2 = angle of refraction; i2 or e = emergent angle; δ = angle of deviation
Relation between angle of incidence, angle of deviation and angle of prism
In ∆O’QR,
Exterior angle = δ

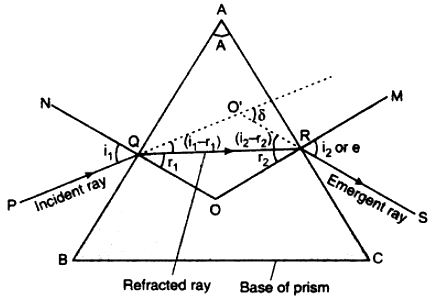
Angle of Minimum Deviation (δm): If the graph is plotted between different incident angles and corresponding angles of deviation, the obtained curve will be as shown in fig. It is clear from the curve that angle of deviation first decreases with increasing angle of incidence and reaches a minimum value 8m and then increases. Clearly, any given value of 8 corresponds to two angles of incidence i1 and i2. This fact is expected from the symmetry of i1 and i2 in equation:
i.e., δ remains the same as i1 and i2 are interchanged. Physically it means that the path of the ray in fig can be traced back resulting the same angle of deviation.
“The minimum value of the angle of deviation suffered by a ray on passing through a prism is called the angle of minimum deviation and is denoted by δm.”
When i1 = i2, then r1 = r2.
Hence in the state of minimum deviation :
(i) Angle of incidence is equal to angle of emergence.
(ii) The refracted ray is parallel to the base of the prism.
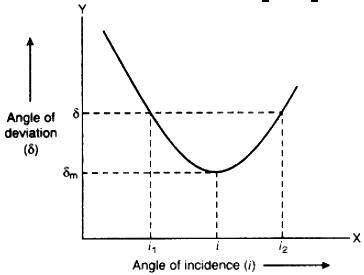
Formula for Refractive Index of the Prism:
Since in state minimum deviation,
i1 = i2 = i and r1 = r2 = r,
The ray diagram through prism is shown in fig
According to Snell’s law, the refractive index of the substance of the prism.