Question

Find equation of tangent and normal following curves, at given points.

(a) y = 2x² - 3x - 1, at (1, - 2)

(b) x = at², y = 2at, t = 1

(c) x = θ + sinθ, y = 1 - cosθ, at θ = π/2

Answer 1

(a) Given curve, 

y = 2x² - 3x - 1 ....(i)

Diff w.r.t. 'x'

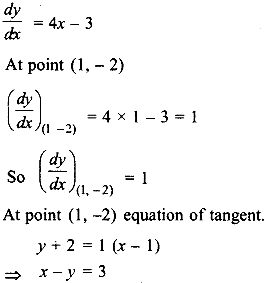
Hence, equation of tangent x - y = 3.

Again, at point (1, -2) equation of normal

y + 2 = - 1(x - 1)

⇒ x + y + 1 = 0

Hence equation of normal x + y + 1 = 0.

(b) Given

x = at², y = 2at .....(i)

Diff. w.r.t. 't'

Equation of tangent

y – 2at = 1 (x – at²)

At t = 1

y – 2a = x – a

⇒ x – y + a = 0

Hence, equation of tangent x – y + a = 0

Again, equation of normal

y – 2at = – 1 (x – a t²)

At t = 1

y – 2a = – (x – a)

⇒ x + y – 3a = 0

Hence, equation of normal x + y – 3a = 0

(c) Given,

x = θ + sin θ, y = 1 – cos θ

Diff. w.r.t. θ,

Hence, equation of tangent x - y = π/2

Again, equation of normal