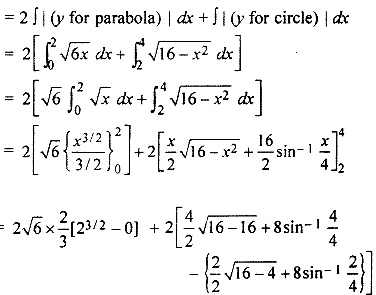Question

Find the area of the common region bounded by x² + y² = 16 and parabola y² = 6x.

Answer 1

Centre of circle x² + y² = 16 is origin and radius is 4 unit.

Vertex of parabola y² = 6x is origin. Common part of these curves is shown in figure.

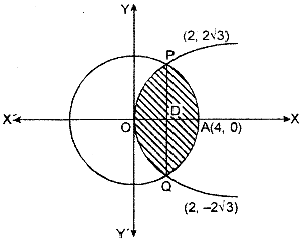
Two curves intersect at point P and Q by solving equations, coordinates of these can be obtained.

Equation of curves x² + y² = 16 …..(i)

y² = 6x …..(ii)

Thus coordinates of ponits P  and Q are (2, 2√3) and (2, - 2√3).

Both the curves are symmetric about x-axis

∴ Required area = Area of OQAPO

= 2 x Area of ODAPO

= 2[Area of ODPO + Area of DAPD]