Question

Differentiate between elastic, inelastic and completely inelastic collisions. Obtain the formula for the velocities of the particles after collision, undergoing head-on collision (elastic).

Answer 1

One Dimensional Elastic Collision
Suppose two bodies of masses m₁ and m₂ be moving in a straight line with velocities u₁ and u₂ respectively and collide with each other. Let their velocities after collision he u₂ and u₂ respectively.

Inelastic collision both momentum and kinetic energy are conserved. Hence, according to the law of conservation of momentum.

In this way, in a one-dimensional elastic collision, the velocity of approach (u₁ – u₂) is equal to the velocity of separation (u₂ -u₁). Hence, the coefficient of restìtutinn is:

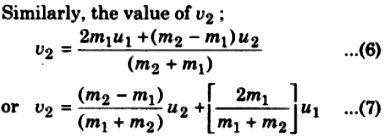
Special Cases:
Case I:
When m₁ = m₂ = m then from Eq. (5) and (7)

Hence, it is clear that there is exchange of velocities in the elastic collision of same masses.

If u₂ = O then u₁ = O and u = u₁ ………………………..(8)

i. e., if the second particle is in the state of rest then after the collision the first particle will remain at rest and second particle will move with the velocity of the first. In this situation the exchange of velocities in both the particles is maximum.

Case II:

So, the heavier mass is undisturbed while the lighter mass reverses its velocity.

Case III:

So, the final velocity of the heavier mass is equal to its initial velocity while the lighter mass moves double of its initial velocity.