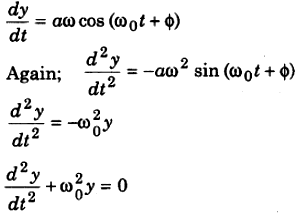Periodic motion : Any motion that repeats itself after regular intervals of time is known as a periodic motion. For example motion of planets around the sun, motion of hands of a clock.
Simple harmonic motion : The to and fro motion about a definite point and of a definite time period along a straight line is called simple harmonic motion. For example, oscillation of a simple pendulum of small amplitude.
Simple harmonic motion is given as F = -ky and in this;
(i) Motion is always in a simple straight line and to and fro of a definite point.
(ii) The direction of acceleration of the moving objects always directed towards the equilibrium state.
(iii) In every position of oscillation the acceleration of the particle is directly proportional to the displacement of the object from its equilibrium state.
Equation of Simple Harmonic Motion :
Suppose any particle oscillates to and fro motion about its equilibrium position. Assuming that at any instant the displacement of the particle is y

If m is the mass of the particle, then working restoring force on the particle F = -ky
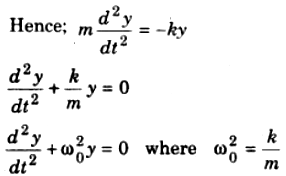
Eq. (S.H.M) is called the equation for linear simple harmonic motion.
The solution of Eq. is represented as follows:
y = α sin (ω0t + Φ)
where α = amplitude and (ω0t + Φ) is the phase angle.
To show that the above equation is the solution of Eq. (S.H.M); we differentiate the equation.