Question

The shadow of a vertical tower on level ground is increased by 40 m, when the altitude of the sun changes from 60° to 30°. Find the height of the tower.

Answer 1

Let CD is a tower of height h. 

Let from its base C, a point B with distance x, the angle of elevation of top of tower is 60°.

When shadow of tower becomes 40 meter more from B than angle of elevation from A becomes 30°.

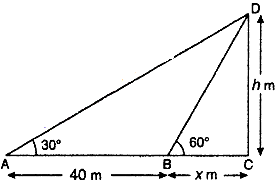
Let BC = x m and ∠CBD = 60°, ∠CAD = 30°

From right angled ∆BCD,

tan 60° = h/x

⇒ √3 = h/x

⇒ x = h/√3

From right angled ∆ACD

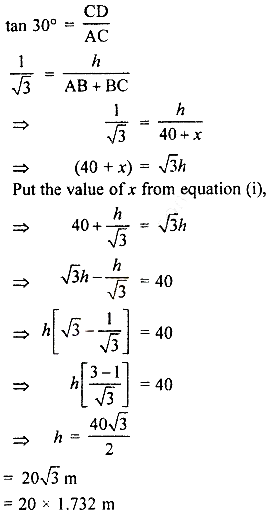
= 34.64 m

Hence, height of tower is 34.64 m