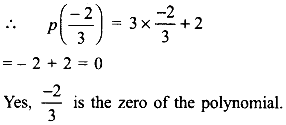(i) p(x) = x2 – 1; x = 1,-1
p(x) = x2 – 1; x = 1, – 1
∴ p(1) = (1)2 – 1
= 1 – 1 = 0
p(- 1) = (- 1)2 – 1
= 1 – 1 = 0
Yes, both 1,-1 are zeroes of the polynomials p(x) = x2 – 1.
(ii) p(x) = 2x + 1; x = \(x=\frac { -1 }{ 2 }\)

(iii) p(x) = 4x + 5; \(x=\frac { -5 }{ 4 }\)
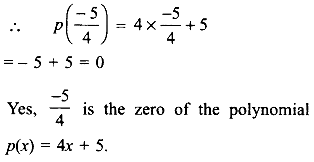
(iv) p(x) = 3x2; x = 0

(v) p(x) = (x – 3)(x + 5); x = 3, – 5
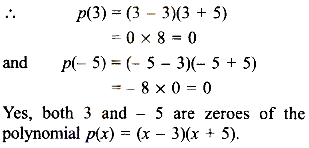
(vi) p(x) = ax + b; \(x=\frac { -b }{ a }\)
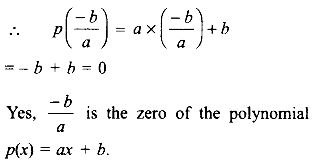
(vii) p(x) = 3x2 – 1; \(x=\frac { -1 }{ \sqrt { 3 } } ,\frac { 1 }{ \sqrt { 3 } } \)
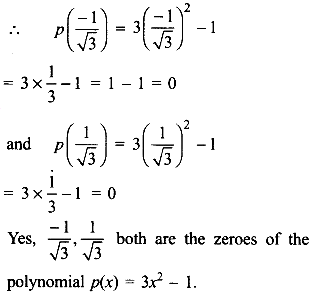
(viii) p(x) = 3x + 2; \(x=\frac { -2 }{ 3 }\)