Question

Solve the following equations.

i. (x² + 12x - 20)/(3x - 5) = (x² + 8x + 12)/(2x + 3)

ii. (10x² + 15x + 63)/(5x² - 25x + 12) = (2x + 3)/(x - 5)

iii. ((2x² + 1)² + (2x - 1)²)/((2x + 1)² - (2x - 1)²) = 17/8

iv. (√(4x + 1) + √(x + 3))/(√(4x + 1) - √(x + 3)) = 4/1

v. ((4x + 1)² + (2x + 3)²)/(4x² + 12x + 9) = 61/36

vi. ((3x - 4)³ - (x + 1)³)/((3x - 4)³ + (x + 1)³) = 61/189

Answer 1

This equation is true for x = 0 

∴ x = 0 is one of the solutions. 

If x ≠ 0, then x² ≠ 0

… [Dividing both sides by x²] 

∴ 8x + 12 = 12x – 20 

∴ 12 + 20 = 12x – 8x

∴ 32 = 4x 

∴ x = 8 

∴ x = 0 or x = 8 are the solutions of the given equation.

So, 2(2x + 1)²/2(2x - 1)² = 25/9

Therefore, (2x + 1)²/(2x - 1)² = 25/9

(2x + 1)/(2x - 1) = ± (5/3)

... [Taking square root of both sides]

... [squaring both sides]

∴ 9(4x + 1) = 25(x + 3) 

∴ 36x + 925x + 75 

∴ 36x – 25 = 75 – 9 

∴ 11x = 66 

∴ x = 6 

∴ x = 6 is the solution of the given equation.

Thus, x = 9/14 or x = - 21/34 is the solution of the given equation.

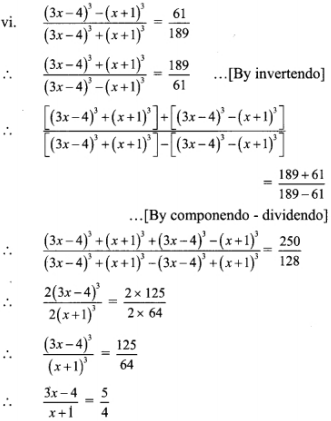
... [Taking cube root of both sides]

∴ 4(3x – 4) = 5(x + 1 ) 

∴ 12x – 16 = 5x + 5 

∴ 12x – 5x = 5 + 16 

∴ 7x = 21 

∴ x = 3 

∴ x = 3 is the solution of the given equation.