The meter bridge is another form of Wheatstone’s bridge. It consists of a uniform manganin wire AB of one meter length. This wire is stretched along a meter scale on a wooden board between two copper strips C and D. Between these two copper strips another copper strip E is mounted to enclose two gaps G1 and G2 An unknown resistance P is connected in G1 and a standard resistance Q is connected in G2.
A jockey (conducting wire) is connected to the terminal E on the central copper strip through a galvanometer (G) and a high resistance (HR). The exact position of jockey on the wire can be read on the scale. A Lechlanche cell and a key (K) are connected across the ends of the bridge wire.
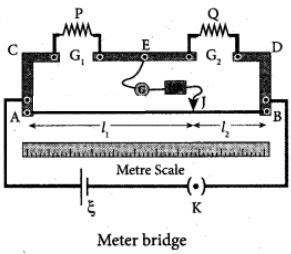
The position of the jockey on the wire is adjusted so that the galvanometer shows zero deflection. Let the point be J. The lengths AJ and JB of the bridge wire now replace the resistance R and S of the Wheatstone’s bridge. Then

The bridge wire is soldered at the ends of the copper strips. Due to imperfect contact, some resistance might be introduced at the contact. These are called end resistances. This error can be eliminated, if another set of readings are taken with P and Q interchanged and the average value of P is found.
To find the specific resistance of the material of the wire in the coil P, the radius r and length l of the wire is measured. The specific resistance or resistivity r can be calculated using the relation
Resistance = ρ - \(\frac{l}{A}\) By rearranging the above equation, we get
ρ = Resistance x\(\frac{A}{l}\) …….. (4)
If P is the unknown resistance, equation (4) becomes
ρ = P\(\frac{πr^2}{l}\)