Question

In a particular university, 40% of the students are having newspaper reading habit. Nine university students are selected to find their views on reading habit. Find the probability that 

(i) none of those selected has newspaper reading habit 

(ii) all those selected have newspaper reading habit 

(iii) at least two-third have newspaper reading habit.

Answer 1

Let X be the binomial random variable which denotes the number of students having newspaper reading habits. 

It is given that 40% of students have reading habit. 

p = = 0.4 and q = 1 – 0.4 = 0.6 

(i) P(none of selected have newspaper reading habit) = P(X = 0) 

Now X ~ B (9, 0.4) 

The p.m.f is given by P (X = x) = p (x) =  ⁹C_x(0.4)^x (0.6)^{9 - x}

P(X = 0) = ⁹C₀(0.4)⁰ (0.6)⁹ = (0.6)⁹ = 0.01008 (using calculator) 

(ii) P (all selected have newspaper reading habit) 

= P (X = 9) 

= ⁹C₉(0.4)⁹ (0.6)⁰ 

= (0.4)⁹ 

= 0.000262 (using calculator) 

(iii) P (at least two third have newspaper reading habit) = P (X ≥ 6) 

{9 students are selected. Two third of them means 2/3 (9) = 6} 

Now P (X ≥ 6) = P (X = 6) + P (X = 7) + P (X = 8) + P (X = 9)

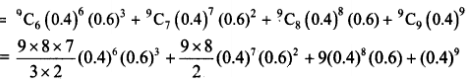
= (84) (0.004096) (0.216) + 36 (0.0016384) (0.36) + 9 (0.00065536) (0.6) + 0.000262 

= 0.074318 + 0.021234 + 0.003539 + 0.000262 

= 0.099353