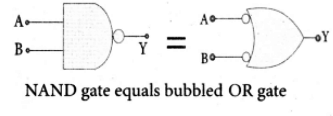De Morgan’s First Theorem:
The first theorem states that the complement of the sum of two logical inputs is equal to the product of its complements.
Proof:
The Boolean equation for NOR gate is Y = \(\overline{A+B}\) . The Boolean equation for a bubbled AND gate is Y =\(\bar{A}\) .\(\bar{B}\) . Both cases generate same outputs for same inputs. It can be verified using the following truth table.
| A |
B |
A + B |
\(\overline{A+B}\) |
\(\bar{A}\) |
\(\bar{B}\) |
\(\bar{A}\).\(\bar{B}\) |
| 0 |
0 |
0 |
1 |
1 |
1 |
1 |
| 0 |
1 |
1 |
0 |
1 |
0 |
0 |
| 1 |
0 |
1 |
0 |
0 |
1 |
0 |
| 1 |
1 |
1 |
0 |
0 |
0 |
0 |
From the above truth table, we can conclude \(\overline{A+B}\) = \(\bar{A}\) . \(\bar{B}\) . Thus De Morgan’s First Theorem is proved. It also says that a NOR gate is equal to a bubbled AND gate. The corresponding logic circuit diagram is shown in figure.

De Morgan’s Second Theorem:
The second theorem states that the complement of the product of two inputs is equal to the sum of its complements.
Proof:
The Boolean equation for NAND gate is Y = \(\overline{AB}\) The Boolean equation for bubbled OR gate is Y = \(\bar{A}\)+ \(\bar{B}\) . A and B are the inputs and Y is the output. The above two equations produces the same output for the same inputs. It can be verified by using the truth table.
| A |
B |
A.B |
\(\overline{A+B}\) |
\(\bar{A}\) |
\(\bar{B}\) |
\(\bar{A}\)+\(\bar{B}\) |
| 0 |
0 |
0 |
1 |
1 |
1 |
1 |
| 0 |
1 |
0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
0 |
0 |
0 |
0 |
From the above truth table we can conclude \(\overline{A.B}\) = \(\bar{A}\) + \(\bar{B}\). Thus De Morgan’s Second Theorem is proved. It also says, a NAND gate is equal to a bubbled OR gate. The corresponding logic circuit diagram is shown in figure.