Consider an object moving in a straight line with uniform or constant acceleration ‘a’. Let u be the velocity of the object at time t = 0, and v be velocity of the body at a later time t.
Velocity – time relation:
(1) The acceleration of the body at any instant is given by the first derivative of the velocity with respect to time,
a = \(\frac{dv}{dt}\) or dv = adt
Integrating both sides with the condition that as time changes from 0 to t, the velocity changes from u to v. For the constant acceleration,

(2) The velocity of the body is given by the first derivative of the displacement with respect to time.
v = or ds = vdt
and since v = u + at,
we get ds = (u+ at ) dt
Assume that initially at time t = 0, the particle started from the origin. At a later time t, the particle displacement is s. Further assuming that acceleration is time-independent, we have

Velocity – displacement relation:
(3) The acceleration is given by the first derivative of velocity with respect to time.
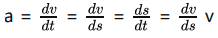
[since ds/dt = v] where s is displacement traverse
This is rewritten as a = \(\frac {1}{2}\)\(\frac{dv^2}{ds}\) or ds = \(\frac{1}{2}\) d (\(v^2\))
Integrating the above equation, using the fact when the velocity changes from u2 to v2, displacement changes from 0 to s, we get

We can also derive the displacement 5 in terms of initial velocity u and final velocity v. From equation we can write,
at = v – u
Substitute this in equation, we get
