Consider a liquid flowing steadily through a horizontal capillary tube. Let v = \((\frac{v}{T})\) be the volume of the liquid flowing out per second through a capillary tube. It depends on (1) coefficient of viscosity (η) of the liquid, (2) radius of the tube (r), and (3) the pressure gradient \((\frac{P}{l})\) .

Substituting in equation (1)
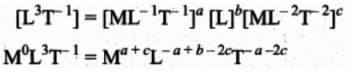
So, equating the powers of M, L and T on both sides, we get
a + c = 0, -a + b – 2c = 3, and – a – 2c = – 1
We have three unknowns a, b and c. We have three equations, on solving, we get
a = – 1, b = 4 and c = 1
Therefore, equation (1) becomes,
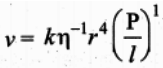
Experimentally, the value of k is shown to be \(\frac{π}{8}\), we have
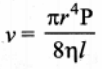
The above equation is known as Poiseuille’s equation for the flow of liquid through a narrow tube or a capillary tube. This relation holds good for the fluids whose velocities are lesser than the critical velocity (vC).