Question

Find the value of  sinA. cosB – cosA. sinB, if tanA = √3 and sinB = 1/2.

Answer 1

Let,

Side opposite to angle θ = 1k

and Hypotenuse = 2k

where, k is any positive integer

So, by Pythagoras theorem, we can find the third side of a triangle

⇒ (AC)² + (BC)² = (AB)²

⇒ (1k)² + (BC)² = (2k)²

⇒ k² + (BC)² = 4k²

⇒ (BC)² = 4k² –k²

⇒ (BC)² = 3 k²

⇒ BC =√3k²

⇒ BC =k√3

So, BC = k√3

Now, we have to find the value of cos B

We know that,

Given: tan A = √3

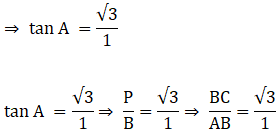
Let,

The side opposite to angle A =BC = √3k

The side adjacent to angle A =AB = 1k

where k is any positive integer

Firstly we have to find the value of AC.

So, we can find the value of AC with the help of Pythagoras theorem

⇒ (AB)² + (BC)² = (AC)²

⇒ (1k)² + (√3k)² = (AC)²

⇒ (AC)² = 1 k² +3 k²

⇒ (AC)² = 4 k²

⇒ AC =√2 k²

⇒ AC =±2k

But side AC can’t be negative. So, AC = 2k

Now, we will find the sin A and cos A

The side adjacent to angle A = AB =1k

Hypotenuse = AC =2k