Question

In the adjoining figure, there are three semi-circles in which BC = 6 cm and BD = 6√3 cm. What is the area of the shaded region in cm² ?

Answer 1

Given:

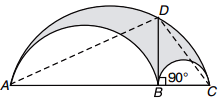
Join DA and DC. 

∠ADC = 90º (Angle in a semi-circle is a right angle). 

∴ AB. BC = BD² 

[From Geometry, BD is the mean proportional between AB and BC.]

⇒ AB. 6 = ( 6 \(\sqrt{3}\) )²  ⇒ AB = 18 cm

∴ Diameter of largest circle = AB + BC = (18 + 6) cm = 24 cm

∴ Area of shaded region 

= Area of largest semi-circle – Sum of the areas of two smaller semi-circles

= \(\frac{\pi \times {12}^2}{2}\) - \(\big(\) \(\frac{\pi \times {9}^2}{2}\) + \(\frac{\pi \times {3}^2}{2}\) \(\big)\) = 72π – 45π

= 27π cm².