Question

A regular hexagon is inscribed in a circle of radius R. Another circle is inscribed in the hexagon. Now another hexagon is inscribed in the second (smaller) circle. What is the ratio of the area of the inner circle to the outer circle?

(a) 3 :4 

(b) 9 :16 

(c) 3 : 8 

(d) None of these

Answer 1

Answer : (a) 3: 4

Each side of the outer (larger) hexagon is equal to the radius of the circle which is R. 

Now OC = ON = OD = radii of smaller circle.

But \(\frac{ON}{OA}\) = sin 60º = \(\frac{\sqrt {3}}{2}\) 

⇒ ON = \(\frac{\sqrt {3}}{2}\) OA = \(\frac{\sqrt {3}}{2}\)R 

= each side of inner hexagon

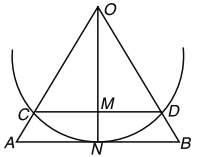
∴ Required ratio = \(\frac{\text{Area of inner circle}}{\text{Area of outer circle}}\) 

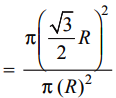
= \(\frac{3}{4}\)