Find the shortest distance between the lines vector r = 3i + 2j - 4k + λ(i + 2j + 2k) and vector r = 5i - 2j + μ(3i + 2j + 6k)

Question

Find the shortest distance between the lines 

\(\vec{r}\)= \(3\hat{i}+2\hat{j}-4\hat{k}+\lambda(\hat{i}+2\hat{j}+2\hat{k})\)

and \(\vec{r}\)= \(5\hat{i}-2\hat{j}+μ(3\hat{i}+2\hat{j}+6\hat{k})\)

If the lines intersect find their point of intersection

Answer 1

We have 

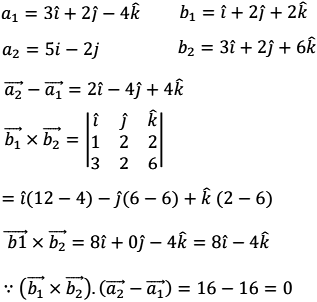
∴ The lines are intersecting and the shortest distance between the lines is 0. 

Now for point of intersection

 

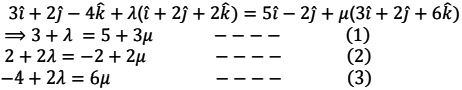
Solving (1) and (2) we get, μ = −2 and λ = −4 

Substituting in equation of line we get

\(\vec{r}\)= \(5i-2j+(-2)(3\hat{i}+2\hat{j}-6\hat{k})\) = \(-\hat{i}-6\hat{j}-12\hat{k}\)

Point of intersection is (−1, −6, −12)