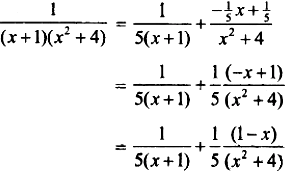Solve into partial fraction for 1/(x^2 + 4)(x + 1)

Question

Solve into partial fraction for \(\frac{1}{(x^2+4)(x+1)}\)

Answer 1

Here the quadratic factor x² + 4 is not factorisable.

Let \(\frac{1}{(x^2+4)(x+1)}\) = \(\frac{A}{x+1}+\frac{Bx+C}{x^2+4}\) ... (1)

Multiply both sides by (x + 1) (x + 4) we get

1 = A(x² + 4) + (Bx + C) (x + 1) … (2) 

Put x = -1 in (2) we get 

1 = A((-1)² + 4) + 0 

1 = A(1 + 4) 

A = \(\frac{1}{5}\)

Equating coefficient of x² on both sides of (2) we get, 

0 = A + B 

0 = \(\frac{1}{5}\) + B 

B = \(\frac{-1}{5}\)

Equating coefficient of x on both sides of (2) we get,

{∵ (Bx + C) (x + 1) = Bx² + Cx = Bx + C} 

0 = B + C 

0 = \(\frac{-1}{5}\) + C 

C = \(\frac{1}{5}\)

Using A = \(\frac{1}{5}\), B = \(\frac{-1}{5}\), C = \(\frac{1}{5}\) we get,