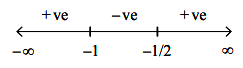\(\frac{x^2+x+1}{x^2+2}\) - \(\frac13\) < 0
⇒ \(\frac{3x^2+3x+3-x^2-2}{3(x^2+2)}<0\) ⇒ \(\frac{2x^2+3x+1}{3(x^2+2)}\) < 0
Now we have to find the range of values in which 2x2 + 3x + 1 < 0 as 3(x2 + 2) is +ve for all real values of x.
Now 2x2 + 3x + 1 < 0 ⇒ 2x2 + 2x + x + 1 < 0
⇒ (2x + 1) (x + 1) < 0 ⇒ \(\big(x+\frac12\big)(x + 1)<0.\)
Critical points are –1 and \(-\frac12\) . Plotting the critical points on the real number line and observing the sign of the expression (2x + 1) (x + 1) in the intervals formed, we see that the expression \(\big(x+\frac12\big)\) (x + 1) is negative or less than zero in the interval \(\big(-1,-\frac12\big)\), , i.e., –1 < x < \(-\frac12.\)
\(x\) ∈ \(\big(-1,-\frac12\big)\)