Proof of the Pythagoras theorem using similarity of triangles.
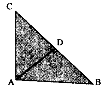
Given: ∠BAC = 90°
To Prove: BC2 = AB2 + AC2
Construction: Draw AD ⊥ BC
Proof:

In ∆ ABC and ∆ DBA
∠B is common and ∠BAC = ∠ADB = 90°
Therefore, ∆ ABC ~ ∆ DBA, (AA similarity)
Hence, the ratio of corresponding sides are equal.
⇒ ABDB = BCBA
⇒ AB2 = BC x DB
Similarity, ∆ ABC ~ ∆ DAC,
⇒ AC/DC = BC/AC
⇒ AC2 = BC x DB
Adding (1) and (2), we get
AB2 + AC2 = BC x DB + BC x DC
= BC x (DB + DC) = BC x BC
⇒ AB2 + AC2 = BC2 and hence the proof of the theorem.