Question

The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the jet plane is flying at a constant height of 1500 3 m, find the speed of the jet plane.

Answer 1

Let BC be the distance covered in 15 seconds.

Also, BE = CD = 1500√3m, be the height of the plane.

Also, ∠EAB = 60^∘ and ∠DAC = 30^∘

In right ΔAEB, we have

tan60^∘ = \(\frac{BE}{AB}\)

⇒ \(\sqrt 3= \frac {1500\sqrt 3}{AB}\)

⇒ AB = 1500 m

In right ΔADC, we have

tan30^∘ = \(\frac {DC}{AC}\)

⇒ \(\frac 1{\sqrt3} = \frac {1500\sqrt 3}{AB + BC}\)

⇒ BC = 1500 × 3 − 1500

⇒ BC = 3000 m

Thus, Speed of the jet plane is = \(\frac{3000}{15}\) = 200 m/s

Answer 2

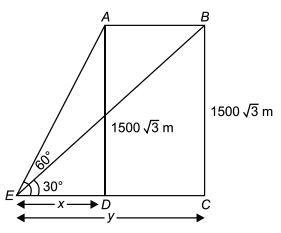
Height of the jet plane = 1500√3 m 

Initially the jet plane is at A and after 15 seconds flight at B.

ED = \(x\), EC = y, where D is right below A and C is right below B 

(the position of the plane after 15 secs).

From ∆EBC, cot 30° = \(\frac{y}{1500\sqrt3}\)

⇒ \(\frac{y}{1500\sqrt3}\) = √3 ⇒ y = 1500 √3 x √3 = 4500 m

From ∆EDA, cot 60° = \(\frac{x}{1500\sqrt3}\) ⇒ \(\frac{x}{1500\sqrt3}\) = \(\frac{1}{\sqrt3}\) ⇒ \(x\) = 1500 m 

∴ AB = DC = Distance travelled in 15 seconds = y – \(x\) = (4500 – 1500) m = 3000 m. 

⇒ Distance travelled in 1 second = \(\frac{3000}{15}\) m = 200 m

Hence speed of the jet plane = 200 m/sec = \(\frac{200}{1000}\) x 60 x 60 km/hr = 720 km/hr.