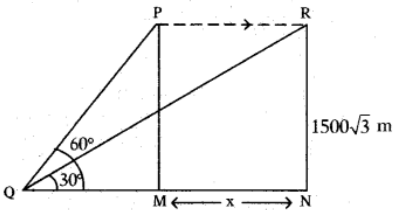
Height of the plane from the ground PM = RN = 1500√3 m.
Angle of elevation are 30° and 60°.
From the figure
tan 60° = \(\frac{PM}{QM}\)
√3 = \(\frac{1500\sqrt{3}}{QM}\)
QM = \(\frac{1500\sqrt{3}}{\sqrt{3}}\) = 1500 m
Also tan 30° = \(\frac{RN}{QN}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{1500\sqrt{3}}{QM+MN}\)
QM + MN = 1500√3 × √3
1500 + MN = 1500 × 3
MN = 4500 – 1500
MN = 3000 mts.
∴ Distance travelled in 15 seconds = 3000 mts.
∴ Speed of the jet plane = \(\frac{distance}{time}= \frac{3000}{15}\) = 200 m/s
= 200 × \(\frac{18}{5}\) kmph
= 720 kmph
Speed = 200 m/sec. or 720 kmph.