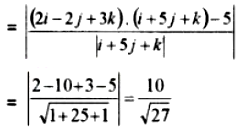Question

Consider a straight line through a fixed point with position vector 2i – 2j + 3k and parallel to i – j + 4k.

1. Write down the vector equation of the straight line. 
2. Show that the straight line is parallel to the plane \(\bar r\).(i + 5y + k) = 5
3. Find the distance between the line and plane.

Answer 1

1. Vector equation of a straight line is \(\bar r\) = \(\bar a\) + λ\(\bar b\) where a is \(\bar a\) fixed point and \(\bar b\) is a vector parallel to the line. Here \(\bar a\) = 2i – 2y + 3 it and \(\bar b\) = i – j + 4k. Therefore vector equation of the line \(\bar r\) = 2i – 2j + 3k + λ(i – j + 4k).

2. The vector parallel to the line is i – j + 4k and vector normal to the plane is i + 5j + k.
Then, (i – j + 4k). (i + 5j + k) = 1 – 5 + 4 = 0
implies that straight line and plane are parallel.

3. A point on the line is 2i – 2j + 3k. Then the distance of 2i – 2j + 3k to the given plane