Question

An automobile company uses three types of steel S₁, S₂ and S₃ for producing three types of cars C₁, C₂ and C₃. 

Steel requirements (in tons) for each type of cars are given below :

Cars	Steel
		C1	C2	C3
S1 S2 S3		2 1 3	3 1 2	4 2 1

Using Cramer’s rule, 

find the number of cars of each type which can be produced using 29, 13 and 16 tonnes of steel of three types respectively.

Answer 1

Given : - 

Steel requirement for each car is given 

Let, Number of cars produced by steel type C₁, C₂ and C₃ be x, y and z respectively. 

Now, 

We can arrange this model in linear equation system 

Thus, 

We have 

2x + 3y + 4z = 29 

x + y + 2z = 13 

3x + 2y + z = 16 

Here,

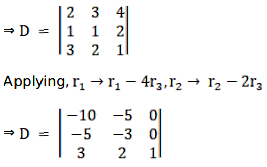
Solving determinant, 

expanding along 3^rd column 

⇒ D = 1[30 – 25] 

⇒ D = 5 

⇒ D = 5 

Again, 

Solve D₁ formed by replacing 1^st column by B matrices 

Here,

Solving determinant, 

expanding along 3^rd column 

⇒ D₁ = 1[( – 35)( – 3) – ( – 5)( – 19)] 

⇒ D₁ = 1[105 – 95] 

⇒ D₁ = 10 

Again, 

Solve D₂ formed by replacing 2^nd column by B matrices 

Here,

Solving determinant, 

expanding along 3^rd column 

⇒ D₂ = 1[190 – 175] 

⇒ D₂ = 15 

And, 

Solve D₃ formed by replacing 3rd column by B matrices 

Here,

Solving determinant, 

expanding along 1^st column 

⇒ D₃ = – 1[ – 23 – ( – 1)3] 

⇒ D₃ = 20 

Thus by Cramer’s Rule, we have

Thus,

Number of cars produced by type C₁, C₂ and C₃ are 2, 3 and 4 respectively.