Question

Differentiate (cos x)^{sin x} with respect to (sin x)^{cos x}.

Answer 1

Let u = (cos x)^{sin x} and v = (sin x)^{cos x}.

We need to differentiate u with respect to v that is find\(\cfrac{du}{d\text x}\).

We have u = (cos x)^{sin x}

Taking log on both sides, we get

log u = log(cos x)^{sin x}

⇒ log u = (sin x) × log(cos x)

[∵ log a^m = m × log a]

On differentiating both the sides with respect to x, we get

Recall that (uv)’ = vu’ + uv’ (product rule)

Now, we have v = (sin x)^{cos x}

Taking log on both sides, we get

log v = log(sin x) cos x

⇒ log v = (cos x) × log(sin x) [∵ log a^m = m × log a]

On differentiating both the sides with respect to x, we get

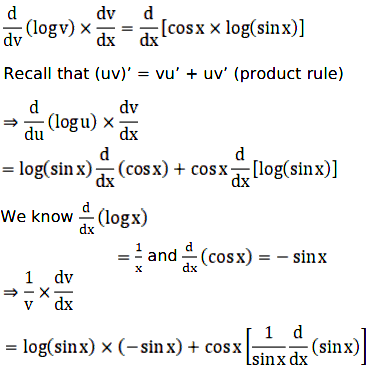
We have