Let u = sin-1\(\Big(2\text x\sqrt{1-\text x^2}\Big)\) and v = sec-1\(\cfrac{1}{\sqrt{1-\text x^2}}\).
We need to differentiate u with respect to v that is find \(\cfrac{du}{dv}
\).
We have sin-1\(\Big(2\text x\sqrt{1-\text x^2}\Big)\)
By substituting x = sin θ, we have
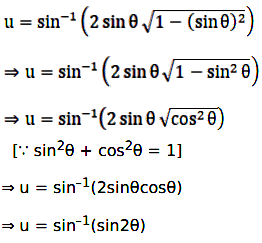
Now, we have v = sec-1\(\cfrac{1}{\sqrt{1-\text x^2}}\).
By substituting x = sin θ, we have
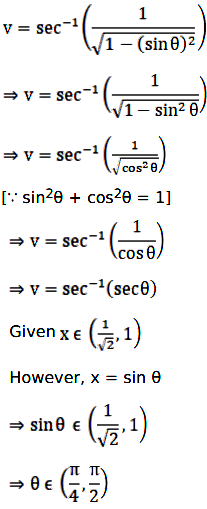

Hence, u = sin–1(sin 2θ) = π – 2θ.
⇒ u = π – 2sin–1(x)
On differentiating u with respect to x, we get

We know \(\cfrac{d}{d\text x}(sin^{-1}\text x)=-\cfrac{1}{\sqrt{1-\text x^2}}
\) and derivative of a constant is 0.

On differentiating v with respect to x, we get
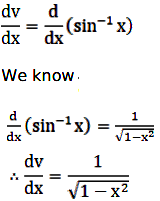
We have
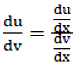
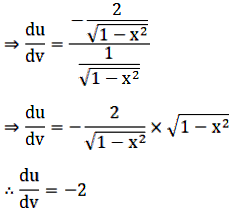
Thus,
\(\cfrac{du}{dv} = -2\)