Question

A tent is in the form of a cylinder of diameter 20 m and height 2.5 m, surmounted by a cone of equal base and height 7.5 m. find the capacity of the tent and the cost of the canvas at Rs. 100 per square metre.

Answer 1

Given: 

A tent is in the form of a cylinder of diameter 20 m and height 2.5 m, surmounted by a cone of equal base and height 7.5 m. 

To find: 

the capacity of the tent and the cost of the canvas at Rs. 100 per square metre. 

Solution:

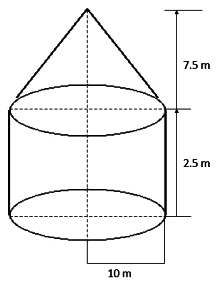
height of Cylinder (h) = 2.5 m 

Radius of cylinder = \(\frac{20}2\) =10 m 

height of cone(h₁) =7.5 m 

Let "l" be the slant height of the cone, As we know l² = \(\sqrt{{r}^2 + h^2}\) 

⇒ l² = \(\sqrt{10^2 + 7.5^2}\)

⇒ l² = \(\sqrt{100 + 56.25}\)

⇒ l² =  \(\sqrt{156.25}\)

⇒ l = 12.5 m 

Volume of a cylinder (v)= πr²h

V₁ = π(10)²(2.5) cm …..(1) 

Volume of cone (V₁) = \(\frac{1}3πr^2h_1\)

Volume of cone (V₁) = \(\frac{1}3π(10)^2\times7.5\)..... (2) 

Volume of boiler = (1) + (2) 

V = V₁ + V₂

v = (π(10)²(2.5)) + \((\frac{1}{3}π(10)^2\times7.5)\)

⇒ V = 250 π + 250 π

⇒ V = 500 π m³ 

Now to find the cost find the curved surface of the tent. CSA of tent 

= CSA of cylinder + CSA of cone = 2πrh + πrl = πr (2h+ l)

= \(\frac{22}{7}\times{10}[2(2.5) + 12.5]\)

= \(\frac{22}{7}\times{10}[5+ 12.5]\)

= \(\frac{22}{7}\times(17.5)\)

= \(\frac{3850}{7}\)

= 550 m² 

Cost of 1 m² canva = Rs 100 

cost of 550 m² canva = 550 × 100 

= Rs 55000