Question

The equation of the curve satisfying the differential equation

y(x + y³)dx = x(y³ – x) dy and passing through the point (1, 1) is

A. y³ – 2x + 3x²y = 0

B. y³ + 2x + 3x²y = 0

C. y³ + 2x – 3x²y = 0

D. None of these

Answer 1

Correct answer is C.

y(x + y³)dx = x(y³ – x)dy

⇒ yx dx + y⁴ dx = xy³ dy – x² dy

⇒ xy³ dy – x² dy – yx dx – y⁴ dx = 0

⇒ y³ [x dy – y dx] – x[x dy + y dx] = 0

Divide both sides by y²x³ we get,

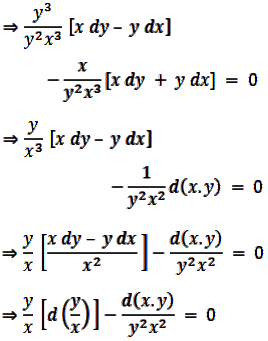
Integrating both sides we get,

Now the given curve is passing through the point (1, 1)

Substituting value of C in (1) we get,

∴ y³ + 2x – 3x²y = 0 is the required solution.