Question

Find the values of a and b for which the system of linear equations has an infinite number of solutions: 

2x + 3y = 7, (a + b)x + (2a - b)y = 21

Answer 1

The given system of equations can be written as 

2x + 3y - 7 = 0 ….(i) 

(a + b)x + (2a - b)y – 21 = 0 ….(ii) 

This system is of the form: 

a₁x+b₁y+c₁ = 0, a₂x+b₂y+c₂ = 0 

where, a₁ = 2, b₁= 3, c₁ = -7 and a₂ = a + b, b₂ = 2a - b, c₂ = – 21 

For the given system of linear equations to have an infinite number of solutions, we must have:

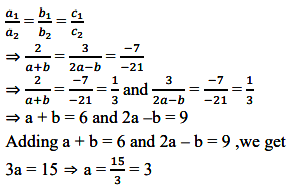
Now substituting a = 5 in a + b = 6, we have 

5 + b = 6 ⇒ b = 6 – 5 = 1 

Hence, a = 5 and b = 1.