Question

The equation of the parabola with focus (0, 0) and directrix x + y = 4 is :

A. x² + y² - 2xy + 8x + 8y - 16 = 0 

B. x² + y² - 2xy + 8x + 8y = 0 

C. x² + y² + 8x + 8y - 16 = 0 

D. x² + y² + 8x + 8y - 16 = 0

Answer 1

Option : (A)

Given that,

We need to find the equation of the parabola with focus (0, 0) and directrix x + y = 4

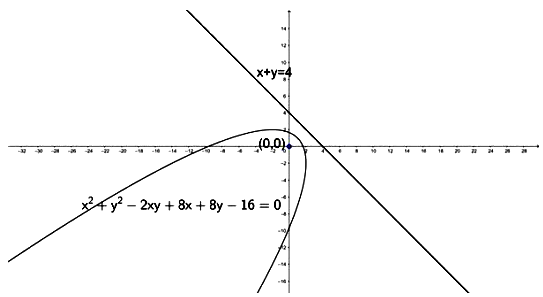
Let us assume P(x, y) be any point on the parabola. 

We know that,

The point on the parabola is equidistant from focus and directrix. 

We know that,

The distance between two points (x₁, y₁) and (x₂, y₂) is \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\).

We know that,

The perpendicular distance from a point (x₁, y₁) to the line ax + by + c = 0 is \(\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\).

⇒ SP = PM 

⇒ SP² = PM²

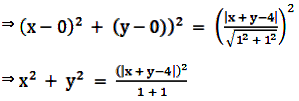
⇒ 2x² + 2y² = x² + y² + 16 + 2xy - 8x - 8y 

⇒ x² + y² - 2xy + 8x + 8y - 16 = 0