Question

Find the modulus of each of the following complex numbers and hence express each of them in polar form: \(\frac{1-i}{1+i}\)

Answer 1

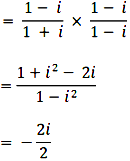
= - i

Let Z = - i = r(cosθ + i sinθ)

Now, separating real and complex part, we get

0 = rcosθ……….eq.1

-1 = rsinθ …………eq.2

Squaring and adding eq.1 and eq.2, we get

1 = r²

Since r is always a positive no., therefore,

r = 1,

Hence its modulus is 1.

Now, dividing eq.2 by eq.1 , we get,

\(\frac{rsin\theta}{rcos\theta}=\frac{-1}{0}\)

Tanθ = - ∞

Since cosθ = 0, sinθ = -1 and tanθ = - ∞,

therefore the θ lies in fourth quadrant.

Tanθ = - ∞, therefore θ = -π/2

Representing the complex no. in its polar form will be

Z = 1{cos(- π/2)+i sin(- π/2)}