(i) Let, x=0.3333…
⇒ x = 0.3+0.03+0.003+…
⇒ x = 3(0.1+0.01+0.001+0.0001+…∞)
⇒ x = 3 (\(\frac{1}{10} + \frac{1}{100} + \frac{1}{1000} + \frac{1}{10000} + .... \infty\))
This is an infinite geometric series.
Here, a = 1/10 and r = 1/10
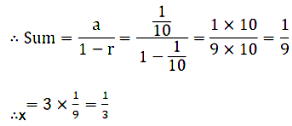
\(\Rightarrow\) 0.\(\bar 3\) = \(\frac{1}{3}\)
(ii) Let, x=0.231231231….
⇒ x=0.231+0.000231+0.000000231+…∞
⇒ x=231(0.001+0.000001+0.000000001+…∞)
⇒ x = 231 (\(\frac{1}{10^3} + \frac{1}{10^6} + \frac{1}{10^9} + \frac{1}{10^{12}}\)+ ....... ∞)
This is an infinite geometric series.
Here, a = \(\frac{1}{10^3}\) and r = \(\frac{1}{10^3}\)
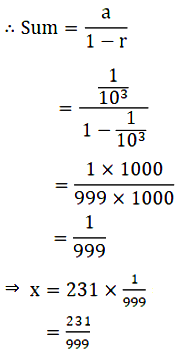
\(\Rightarrow\) 0.\(\overline {231}\) = \(\frac{231}{999}\)
(iii) Let, x=3.525252552…
⇒ x=3+0.52+0.0052+0.000052+…∞
⇒ x=3+52(0.01+0.0001+…∞)
⇒ x=3+52 (\(\frac{1}{10^2} + \frac{1}{10^4} + \frac{1}{10^6} + \frac{1}{10^{8}}\)+....... ∞)
Here, a = \(\frac{1}{10^2}\) and r = \(\frac{1}{10^2}\)


\(\Rightarrow\) 3.\(\overline{52}\) = \(\cfrac{349}{999}\)