Question

Find the values of `m` for which roots of equation `x^(2)-mx+1=0` are less than unity.

Answer 1

Let `f(X)=x^(2)-mx+1` as both roots of `f(x)=0` are less than 1 we can take `Dge0, af(1)ge0` and `-b/(2a)lt1`
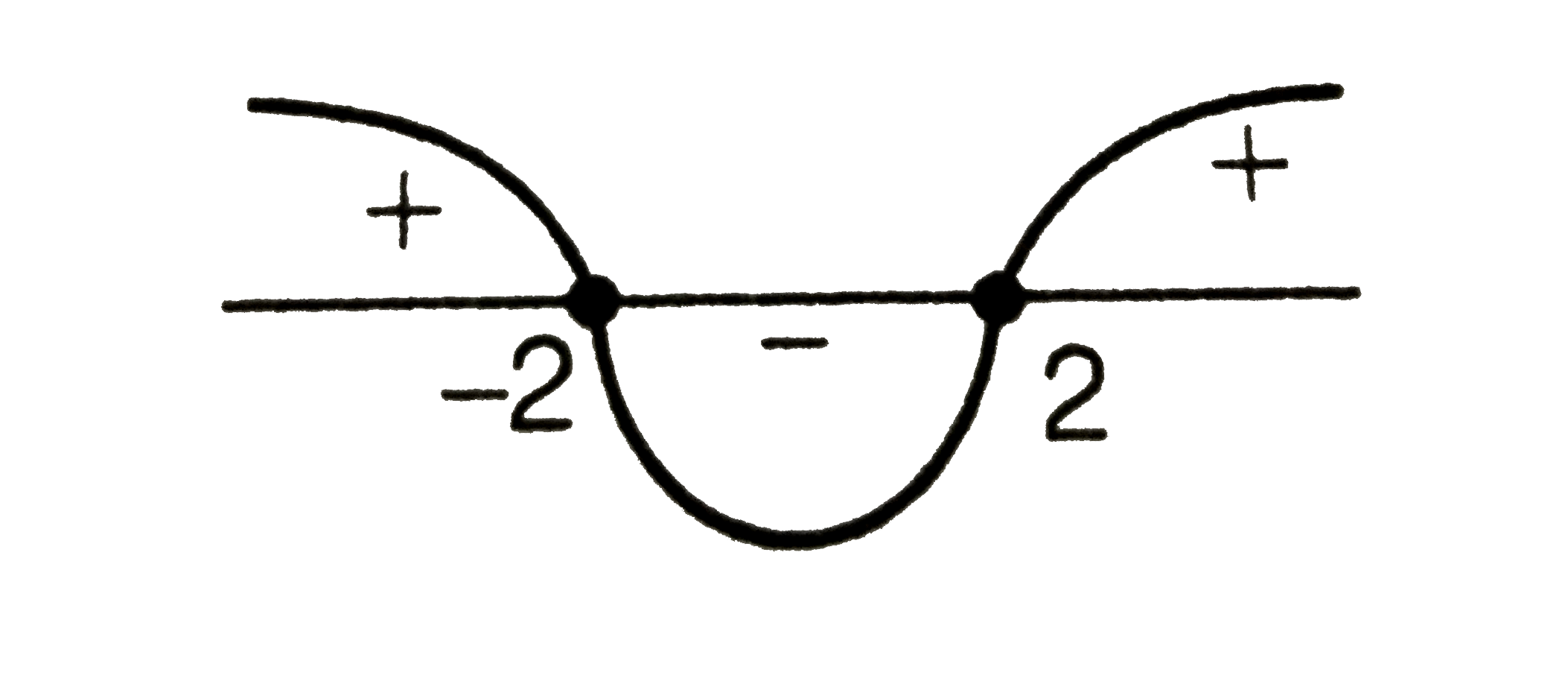
ltBrgt (i) Consider `Dge0(-m)^(2)-4.1.4ge0`
`implies(m+2)(m-2)ge0`
`impliesm epsilon (-oo,-2[uu[2,oo)`…......i
(ii) Consider af `(1) gt01(1-m+1)gt0`
`impliesm-2lt0impliesmlt2`
`impliesm epsilon (-oo,2)` .......ii
(iii) Consider `(-b/(2a)lt1)`
`m/2lt1impliesmlt2`
`impliesm epsilon (-oo,2)`........iii
Hence the values of `m` satisfying Eqs. (i), (ii) and (iii) at the same time are `m epsilon (-oo,-2]`